Knuth-Morris-Pratt (KMP) Algorithm
The Knuth-Morris-Pratt (KMP) algorithm is a string-matching algorithm that efficiently finds occurrences of a pattern within a longer text. It was developed by Donald Knuth and Vaughan Pratt, and independently by James H. Morris in 1977.
The KMP algorithm works by precomputing a partial match table, which tells us how much of the pattern can be skipped when a mismatch occurs during the matching process. The partial match table is computed in linear time with respect to the length of the pattern.
Take your coding skills to the next level with our comprehensive guides, “Python Beginner to Advanced” and “Java Beginner to Advanced.” Whether you’re diving into Python or mastering Java, these books provide step-by-step guidance and in-depth knowledge to elevate your programming expertise.
KMP Algorithm Implementation
Suppose we have two strings named text and pattern. we want to check whether a substring of text is equal to the pattern.
A substring is a contiguous sequence of a string. If a string is “enablegeek” then the substrings of the string are “enablegeek”, “ena”, “geek”, “able” etc. But “eble” , “ane” are not substrings of the string.
Let us have a text “enablegeek” and a pattern “able”. We want to find whether “able” is a substring of “enablegeek” or not.
At first, we will solve it with a naive approach. In the naive approach, if the text length is n and the pattern length is m, then we will take every substring of m length and then check whether this substring is equal to the pattern or not.
bool naive_matching(string text, string pattern)
{
int n=text.size();
int m=pattern.size();
for(int i=0;i<n;i++)
{
// for each position i, we will try to
// match text[i, i+1, i+2, ... i+m-1] with pattern[0, 1, 2, .. m-1]
int j=0;
for(j=0;j<m, i+j<n ;j++)
{
if(pattern[j]!=text[i+j]) break;
}
if(j==m)
{
return true;
}
}
return false;
}The time complexity of the above code is O(n*m).
Now try to simulate this algorithm for the text “abababacd” and the pattern “ababac”.
At first, i=0. We will continue to match the pattern and the text character by character starting from the first character of the text. If all characters match, we get the pattern. And if we get one place where those characters from the text and pattern don’t match we will break the loop. Check out the picture below:
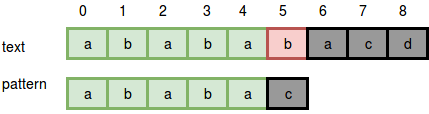
Going to character number 5, we get a mismatch. The loop inside the brute force algorithm will break. Then we will go to i=1 and then search again.
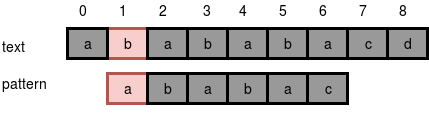
In this way, you have to loop through each index of text to find the pattern, so the time complexity of this approach is O(n*m). If we can avoid looping through each index, we can solve it with better time complexity. For this, we need to know about prefixes and suffixes.
Prefix: When zero or more characters are dropped from the end of a string, what is left is the prefix of the string. Prefixes of string “abc” are “a”, “ab”, “abc”. Among them, “ab” and “a” are proper prefixes. proper prefixes are smaller than the original string.
Suffix: When zero or more characters are dropped from the start of a string, what is left is the suffix of the string. Suffixes of string “abc” are “c”, “bc”, “abc”. among them “c”, “bc” are proper prefixes because they are smaller than the original string.
Assume the pattern we are looking for is “abxyabcd”. Now, look at the picture below.

We found a mismatch in one place when matching the pattern with the text in the image. There is no need to worry about what the mismatched character is or what the next characters are. Now if we try to brute-force match the pattern by shifting it from one position to the left, is there any benefit for us?

If we shift 1 position then whatever is in the question mark places is of no use. How much position shifting can be profitable depends on what? It depends on how many prefixes in the pattern match the text, in this case, that prefix is “ABXYAB”. If we shift as follows we can get a match:

That means we have to shift the pattern in such a way that we get a partial matching of the prefix of the pattern with the suffix of the pattern itself. So what happens is, we get a partial match of the input text with the pattern prefix, and then we go back and do a character-by-character match to see if the entire text matches.
Another example will make it clear. Suppose now the pattern is “ABABAC” and we get a partial matching like this:

Now, how much we shift will depend on the matching prefix “ABABA”. See the picture below:

We have shifted the pattern to the right by 2 spaces. This will give us a partial match of pattern prefix with pattern suffix. In this case, the last 3 characters match the first 3 characters of the pattern. That means the first 3 characters of the pattern will match the text as well. Then we will go ahead again and look at the rest of the characters.
Now suppose unfortunately we get a mismatch again:

How much to shift now? It depends on “ABA”. We need to shift “ABA” to the right such that the suffix of “ABA” partially matches the prefix of “ABA” after the shift. In this case, we have to shift like the picture below.

Now, one thing is clear, how far the pattern will be shifted depends on how many prefixes in the pattern match the text.
Suppose the prefix P of the pattern matches with the text. Now we have to find the largest proper prefix of P which is also a suffix of P.
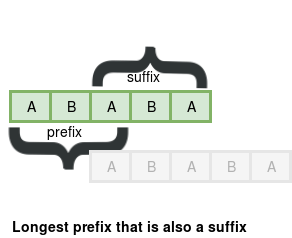
Now, for every proper prefix P, we will find the length of the largest proper prefix which is also a suffix.
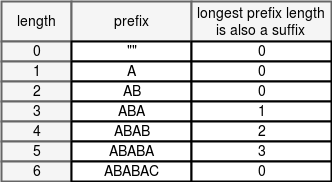
KMP Algorithm is a string-matching algorithm that searches for occurrences of a pattern within a larger text by preprocessing the pattern to determine the maximum suffix that matches a prefix of the pattern. This preprocessed information is then used to avoid unnecessary comparisons when searching for the pattern in the text.
KMP Algorithm in C++
C++ code with explanations:
#include <iostream>
#include <string>
#include <vector>
using namespace std;
void KMP(string text, string pattern)
{
int n = text.length(), m = pattern.length();
// calculate the prefix table
vector<int> pi(m);
pi[0] = 0;
for (int i = 1, j = 0; i < m; i++) {
while (j > 0 && pattern[i] != pattern[j])
j = pi[j - 1];
if (pattern[i] == pattern[j])
j++;
pi[i] = j;
}
// search for pattern in the text using the prefix table
for (int i = 0, j = 0; i < n; i++) {
while (j > 0 && text[i] != pattern[j])
j = pi[j - 1];
if (text[i] == pattern[j])
j++;
if (j == m) {
cout << "Pattern found at index " << i - m + 1 << endl;
j = pi[j - 1];
}
}
}
int main()
{
string text, pattern;
cout << "Enter text: ";
getline(cin, text);
cout << "Enter pattern: ";
getline(cin, pattern);
KMP(text, pattern);
return 0;
}
The function KMP takes in two strings, text and pattern, which represent the text to search and the pattern to find, respectively. The lengths of the text and pattern strings are stored in variables n and m, respectively. The prefix table pi is calculated using the pattern string. The prefix table is used to determine the maximum suffix of the pattern that matches a prefix of the pattern. The prefix table is represented by a vector pi of length m. The first element of pi is always 0.
A loop is used to fill in the rest of the prefix table by comparing each character of the pattern with the character at the current index of the prefix table. If they match, the value of j is incremented, and the value of j is stored in pi[i]. If they don’t match, j is set to the value of pi[j-1], and the loop continues until a match is found or j becomes 0.
The for loop is used to search for the pattern in the text using the prefix table. The loop iterates through each character of the text string. If the character at the current index of the text string matches the character at the current index of the pattern string, the value of j is incremented. If they don’t match, j is set to the value of pi[j-1], and the loop continues until a match is found or j becomes 0.
If the value of j is equal to the length of the pattern string, then a match has been found, and the index of the first occurrence of the pattern in the text is printed. The value of j is then set to the
KMP Algorithm in Python
Python code with explanations:
def kmp_search(text, pattern):
matches = []
n, m = len(text), len(pattern)
lps = compute_lps(pattern)
i, j = 0, 0
while i < n:
if text[i] == pattern[j]:
i += 1
j += 1
if j == m:
matches.append(i - j)
j = lps[j - 1]
elif i < n and text[i] != pattern[j]:
if j != 0:
j = lps[j - 1]
else:
i += 1
return matches
def compute_lps(pattern):
m = len(pattern)
lps = [0] * m
len = 0
i = 1
while i < m:
if pattern[i] == pattern[len]:
len += 1
lps[i] = len
i += 1
else:
if len != 0:
len = lps[len - 1]
else:
lps[i] = len
i += 1
return lps
The code implements the Knuth-Morris-Pratt (KMP) algorithm for pattern searching in a given text.
The KMP algorithm is an efficient pattern-matching algorithm that uses a precomputed table called the Longest Prefix-Suffix (LPS) array. The LPS array stores the length of the longest proper prefix of the pattern that is also a suffix of the pattern.
The kmp_search() function takes two arguments – the text in which the pattern is to be searched and the pattern that needs to be searched. The function initializes an empty list matches to store the starting indices of all the matches found.
The function calls compute_lps() function to precompute the LPS array for the pattern. It then initializes two indices i and j to 0 to traverse through the text and pattern respectively.
In the while loop, the function compares the characters of the text and pattern at indices i and j respectively. If they match, it increments both indices, and if j becomes equal to the length of the pattern, the function appends i – j to the matches list and updates j to lps[j-1].
If the characters don’t match, the function checks if j is not zero. If it is not zero, then it updates j to lps[j-1] and if it is zero, then it increments i. The function continues this process until it has traversed the entire text.
The compute_lps() function computes the LPS array for a given pattern. It initializes an empty list lps of length m (the length of the pattern) and initializes two variables len and i to 0 and 1 respectively.
In the while loop, the function compares the characters of the pattern at indices i and len. If they match, it increments len and sets lps[i] to len. It then increments i.
If the characters don’t match, the function checks if len is not zero. If it is not zero, then it updates len to lps[len-1] and the loop continues. If it is zero, then it sets lps[i] to len and increments i. The function continues this process until it has computed the LPS array for the entire pattern.
KMP Algorithm in Java
Java code with explanations:
import java.util.*;
public class KMP {
public static List<Integer> kmpSearch(String text, String pattern) {
List<Integer> matches = new ArrayList<>();
int n = text.length();
int m = pattern.length();
int[] lps = computeLPS(pattern);
int i = 0, j = 0;
while (i < n) {
if (text.charAt(i) == pattern.charAt(j)) {
i++;
j++;
}
if (j == m) {
matches.add(i - j);
j = lps[j - 1];
} else if (i < n && text.charAt(i) != pattern.charAt(j)) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}
return matches;
}
public static int[] computeLPS(String pattern) {
int m = pattern.length();
int[] lps = new int[m];
int len = 0, i = 1;
lps[0] = 0;
while (i < m) {
if (pattern.charAt(i) == pattern.charAt(len)) {
len++;
lps[i] = len;
i++;
} else {
if (len != 0) {
len = lps[len - 1];
} else {
lps[i] = len;
i++;
}
}
}
return lps;
}
}
You can follow the previous explanation as well.



