Ternary Search

Let us have a function y=f(x)=3+x-x*x. We want to find x for which y is maximum

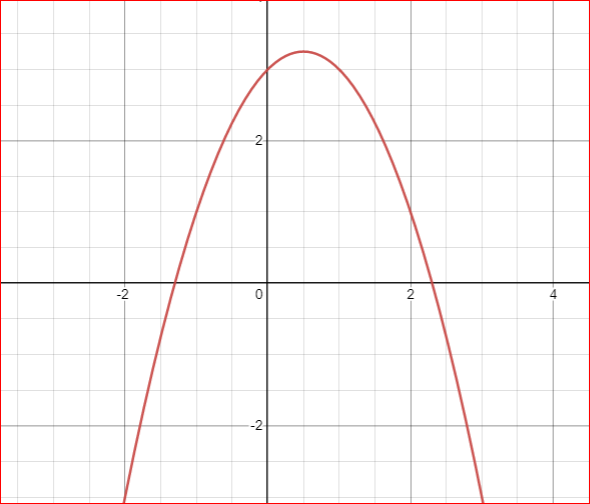
In this graph, we can see if you increase x first y is increasing and then y is decreasing.
If some graph is first increasing and then decreasing or first decreasing and then increasing in a range then we can apply ternary search.
First, pick a range where the maximum exists. let’s say the range is from l=-10000 to r=10000.
We are not trying to find the exact point, we will consider an error less than or equal to 0.01.
For every iteration, we will divide the range into 3 parts, let’s say ranges are [l, m1], (m1, m2], (m2, r].
Then compare f(m1) and f(m2). if f(m1) is greater than f(m2) than maximum is in range [l, m2] otherwise it is in [m1, r]. In this way, the range will converge and we will find the maximum value of y.

Ternary Search in c++

#include<bits/stdc++.h>
using namespace std;
double f(double x)
{
    return 3+x-x*x;
}
int main()
{
    double l=-10000, r=10000;
    while(r-l>0.01)
    {
        double m1=l+(r-l)/3.0;
        double m2=r-(r-l)/3.0;
        if(f(m1)>f(m2))
        {
            r=m2;
        }
        else l=m1;
    }
    cout<<l<<endl;
}

Ternary Search in Python

def f(x):
    return 3+x-x*x

l, r=-1000, 1000
while r-l>0.01:
    m1=l+(r-l)/3
    m2=r-(r-l)/3
    if f(m1)>f(m2):
        r=m2
    else:
        l=m1

print(l)