Let us have a function y=f(x)=3+x-x*x. We want to find x for which y is maximum
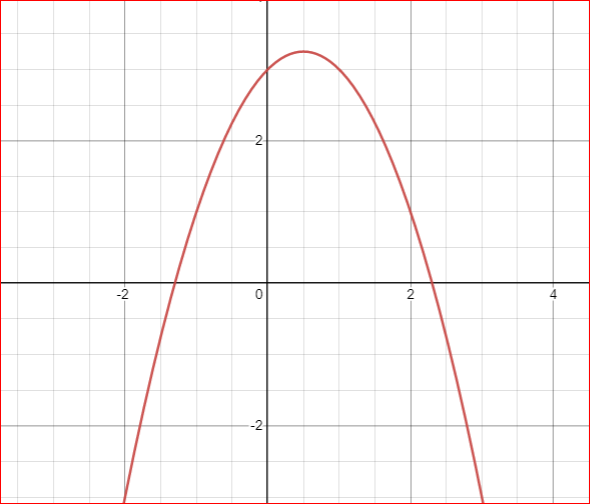
In this graph, we can see if you increase x first y is increasing and then y is decreasing.
If some graph is first increasing and then decreasing or first decreasing and then increasing in a range then we can apply ternary search.
First, pick a range where the maximum exists. let’s say the range is from l=-10000 to r=10000.
We are not trying to find the exact point, we will consider an error less than or equal to 0.01.
For every iteration, we will divide the range into 3 parts, let’s say ranges are [l, m1], (m1, m2], (m2, r].
Then compare f(m1) and f(m2). if f(m1) is greater than f(m2) than maximum is in range [l, m2] otherwise it is in [m1, r]. In this way, the range will converge and we will find the maximum value of y.
Ternary Search in C++
#include<bits/stdc++.h>
using namespace std;
double f(double x)
{
return 3+x-x*x;
}
int main()
{
double l=-10000, r=10000;
while(r-l>0.01)
{
double m1=l+(r-l)/3.0;
double m2=r-(r-l)/3.0;
if(f(m1)>f(m2))
{
r=m2;
}
else l=m1;
}
cout<<l<<endl;
}This is a C++ program that uses the ternary search algorithm to find the minimum value of a given function.
The program defines a function f which takes in a double value x and returns the value of 3+x-x*x. This function is the one whose minimum value we want to find using ternary search.
The ternary search algorithm is implemented using a while loop that continues until the difference between r and l becomes less than or equal to 0.01 (which is our desired precision). In each iteration of the loop, two new points m1 and m2 are calculated as follows: m1=l+(r-l)/3.0 and m2=r-(r-l)/3.0. These two points divide the range [l, r] into three parts of equal width.
We then compare the values of f(m1) and f(m2) to determine which part of the range to discard. If f(m1) is greater than f(m2), then we know that the minimum value lies in the range [m1, r], so we discard the left part of the range by setting l=m1. Otherwise, we know that the minimum value lies in the range [l, m2], so we discard the right part of the range by setting r=m2.
The program prints the value of l, which is the point at which the function f achieves its minimum value.
Ternary Search in Python
def f(x):
return 3+x-x*x
l, r=-1000, 1000
while r-l>0.01:
m1=l+(r-l)/3
m2=r-(r-l)/3
if f(m1)>f(m2):
r=m2
else:
l=m1
print(l)
This is a Python program that uses the ternary search algorithm to find the minimum value of a given function.
The program defines a function f which takes in a value x and returns the value of 3+x-x*x. This function is the one whose minimum value we want to find using ternary search.
The ternary search algorithm is implemented using a while loop that continues until the difference between r and l becomes less than or equal to 0.01 (which is our desired precision). In each iteration of the loop, two new points m1 and m2 are calculated as follows: m1=l+(r-l)/3.0 and m2=r-(r-l)/3.0. These two points divide the range [l, r] into three parts of equal width.
We then compare the values of f(m1) and f(m2) to determine which part of the range to discard. If f(m1) is greater than f(m2), then we know that the minimum value lies in the range [m1, r], so we discard the left part of the range by setting l=m1. Otherwise, we know that the minimum value lies in the range [l, m2], so we discard the right part of the range by setting r=m2.
Finally, the program prints the value of l, which is the point at which the function f achieves its minimum value. This program demonstrates a basic implementation of the ternary search algorithm in Python.



