We can represent a graph with a matrix. In the unweighted graph, We can create a matrix with 0 and 1. Here 0 means there is no edge and 1 means there is an edge.
For example, we have a graph below,
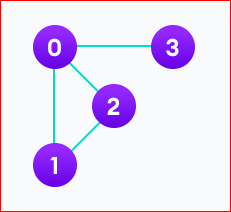
We can represent this graph in matrix form like below.
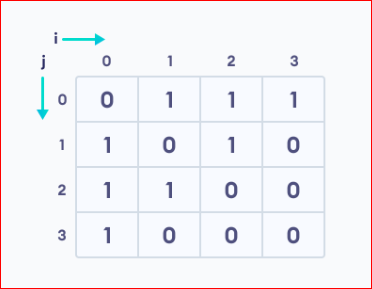
Each cell in the Above matrix is represented as Aij. Here i, and j are vertices, And the value of Aij is either 0 or 1 depending on whether there is an edge from vertice i to j. If there is an edge from i to j, then Aij is 1 otherwise 0.
In a weighted graph, Aij Represents the weight of the edge from vertice i to j.
Adjacency Matrix Code in Python
adjMatrix=[]
n=int(input()) # number of vertices.
m=int(input()) # number of edges
for i in range(n):
adjMatrix.append([0 for _ in range(n)])
# input edge list.
for i in range(m):
a, b=map(int, input().split())
adjMatrix[a][b]=1
adjMatrix[b][a]=1
for i in range(n):
for j in range(n):
print(adjMatrix[i][j], end=' ')
print('')
Adjacency Matrix Code in C++
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m;
cin>>n; // n is the number of vertices
cin>>m; // m is the number of edges
vector<vector<int> > adjMatrix(n, vector<int> (n));
// input edgelist
for(int i=0;i<m;i++)
{
int a, b;
cin>>a>>b;
adjMatrix[a][b]=1;
adjMatrix[b][a]=1;
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cout<<adjMatrix[i][j]<<' ';
}
cout<<endl;
}
return 0;
}



